From Open-Unmix to umx.cpp

Open-Unmix

Open-Unmix aims to be a "reference implementation" of a music source separation neural network. Its impact on modern source separation research (through open source code availability and sponsoring AI competitions) cannot be overstated.

Being an older model, its performance is largely considered outdated these days. In the MDX 2021 challenge, it got beat by 2 dB by Demucs v3, and since then, Demucs v4 is leaps and bounds better.

However, it has an easy-to-understand architecture, and it was the first neural network whose inference I rewrote in C++ to build an earlier version of https://freemusicdemixer.com. In this static site, a WebAssembly/WASM module for music demixing is loaded client-side and run in the user's browser for private, offline, local AI inference.

My site is still around and evolved past Open-Unmix, but this blog post is the story of how Open-Unmix made my website possible and the adaptations I made to the network inference to run lighter and faster in the WebAssembly environment.

umx.cpp

The origin story of umx.cpp is llama.cpp, which was a from-scratch C implementation of the inference of the Meta LLama large language model. I wanted to do the same (mostly as an educational exercise on the internal workings of PyTorch), and picked a neural network I was familiar with, Open-Unmix, as my target to rewrite.

I won't describe the exhaustive steps of how I created umx.cpp - there's a rough sketch in the repo README - but I want to highlight 3 unique differences from the original PyTorch code that are important aspects of umx.cpp and its goals to provide efficient inference in the WebAssembly browser runtime.

Mixed-integer quantization

The biggest, best-performing weights of Open-Unmix are the UMX-L weights. These are 113.1 MB for each of the vocals, drums, bass, and other targets, or 452.4 MB total. Proposing a 400+ MB download for the users of my eventual website seemed like a big issue, and I wanted to tackle model size immediately.

Intro to quantization

When a tensor is quantized, this refers to using a smaller number type to store what was originally their float32 values. For example, this is some pseudocode showing how to quantize float32 values to uint8 and uint16 with numpy:

import numpy as np


def quantize_tensor(x, scale, zero_point, qmin, qmax, dtype):
    x = np.round(x / scale + zero_point)
    x = np.clip(x, qmin, qmax)
    return x.astype(dtype)


def dequantize_tensor(x, scale, zero_point):
    return scale * (x.astype(np.float32) - zero_point)


def compute_scale_zero_point(min_val, max_val, qmin, qmax):
    scale = (max_val - min_val) / float(qmax - qmin)
    zero_point = round(qmin - min_val / scale)
    return scale, zero_point


def quantization_example(tensor):
    data_types = {
        'uint8': (np.uint8, np.iinfo(np.uint8).min, np.iinfo(np.uint8).max),
        'uint16': (np.uint16, np.iinfo(np.uint16).min, np.iinfo(np.uint16).max),
    }

    for name, (dtype, qmin, qmax) in data_types.items():
        min_val, max_val = tensor.min(), tensor.max()
        scale, zero_point = compute_scale_zero_point(min_val, max_val, qmin, qmax)

        q_tensor = quantize_tensor(tensor, scale, zero_point, qmin, qmax, dtype)
        dq_tensor = dequantize_tensor(q_tensor, scale, zero_point)
        error = np.mean(np.abs(tensor - dq_tensor))

        # Compute and print sizes
        original_size = tensor.nbytes
        quantized_size = q_tensor.nbytes + 8 # add 8 bytes for scale and zero-point float32s

        print(f"\t{name} quantization Mean error: {error}")
        print(f"\tOriginal size (bytes): {original_size}, quantized size: {quantized_size}\n")


if __name__ == '__main__':
    n_elems = 256
    tensor_pos = np.linspace(0, 1, num=n_elems, dtype=np.float32)
    tensor_neg = np.linspace(-1, 1, num=n_elems, dtype=np.float32)

    print("Positive [0, 1] tensor with 256 elements")
    quantization_example(tensor_pos)

    print("Positive/negative [-1, 1] tensor with 256 elements")
    quantization_example(tensor_neg)

Positive [0, 1] tensor with 256 elements
        uint8 quantization Mean error: 1.9634171621873975e-08
        Original size (bytes): 1024, quantized size: 264

        uint16 quantization Mean error: 4.638422979041934e-10
        Original size (bytes): 1024, quantized size: 520

Positive/negative [-1, 1] tensor with 256 elements
        uint8 quantization Mean error: 0.003921561408787966
        Original size (bytes): 1024, quantized size: 264

        uint16 quantization Mean error: 1.5259243809850886e-05
        Original size (bytes): 1024, quantized size: 520

Notice approximately 25% space taken by the uint8-quantized tensor and 50% by the uint16-quantized tensor, which is what we expect since float32 are 4 bytes (32 bits) in size, uint16s are 2 bytes (16 bits) in size, and a uint8 is 1 byte (8 bits) in size.

For the positive-only tensor, both uint8 and uint16 show small error (e-8, e-10). Their ranges are [0, 255] and [0, 65535] respectively. For the tensor with mixed positive and negative values, the increased range of the uint16 type results in a lower error (e-5 vs. e-2 of uint8).

Int vs. uint, scale without zero-point?

While researching the material for this blog post, I sort of confused myself. I don't know why I picked uint8 and uint16 and not int8 and int16. I believe that since I'm computing the quantized tensor with the scale and zero-point, the zero-point will inherently be able to adjust any negative range into a positive range.

In my tests, the error between uint8/int8 and uint16/int16 quantization were not distinguishable despite trying to cherry-pick examples. Simply put, if uint8 has a range of [0, 255] and int8 has a range of [-127, 128], but we have:

float value_reconstructed = quantized_value*scale + zero_point

Would simply setting zero_point += 127 not nullify any differences in the uint8 and int8 dtype?

As a counterpoint, here are some interesting slides by NVIDIA describing some hardware details of int8 inference and making a case for getting rid of the zero-point when quantizing. Here's another article that gives good information on the difference between quantizing with and without storing the zero-point or offset.

Mixing uint8 and uint16

In umx.cpp, I can choose to quantize the weights of UMXL from float32 to uint16 or uint8 (along with the stored scale and zero-point or offset value). Empirically (i.e. by trying out different strategies and measuring the final performance of the neural network with several predictable, known examples), I found that I could store every layer of Open-Unmix as uint8 (for 75% space savings), except for the final 2 layers of BatchNorm and FullyConnected (fc2, bn2, fc3, bn3 in the Open-Unmix code), which are the final 4 layers generating the output values, and where quantization errors would have a bigger impact on the output audio waveforms. For those, I quantized as uint16 (or 50% space savings).

That's why I call my strategy "mixed-integer quantization," since I hand-picked which layers needed higher precision in their weights.

The quantized tensors are loaded first into the same datatype of Eigen tensor, then that tensor is cast to a regular float32 tensor. The inference also runs with float32 tensors in Eigen for maximum performance (assuming C++ linear algebra libraries are more optimized for float32 computations than integer). The only purpose of quantized representation is really only for file size savings, not runtime.

Demucs waveform split inference

In a blog post on the freemusicdemixer site, I describe how Demucs splits a waveform into overlapping segments, processes each one independently, and recombines them using a weighted overlap-add procedure with a triangle transition window. This is necessary to avoid boundary artifacts (or audible discontinuities, corruptions, clicks) when recombining two neighboring but independently-modified segments of a waveform.

Illustration:

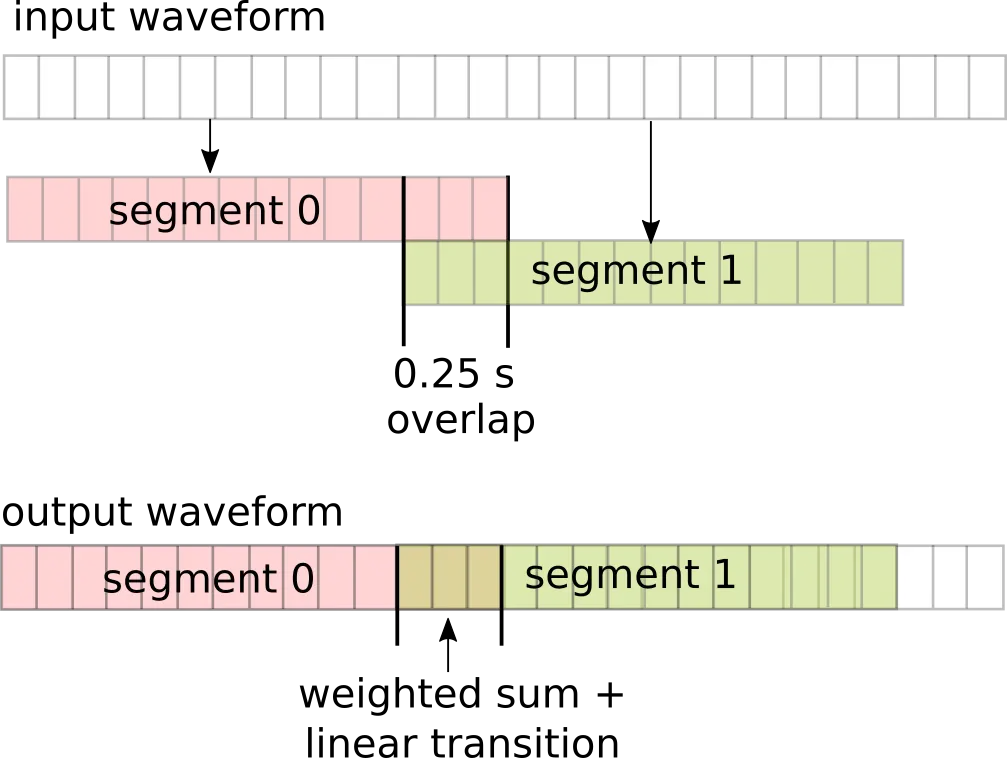
In umx.cpp, I ran into the limitation that trying to demix the entire waveform all at once was predicably exceeding the 4 GB maximum memory limitation of WebAssembly, and I had to do it in sub-parts. Therefore, I implemented Demucs segmentation in umx.cpp - you can see the C++/Eigen code here.

This is not really any part of the Demucs neural network architecture, but an inference helper function to split a long input waveform into fixed-size segments, demix them independently, and recombine those segments with seamlessly blended boundaries. Still, it's useful to keep in one's source separation (or audio processing) toolbox.

We broke the LSTM!

Open-Unmix uses a long-short-term memory module. When Open-Unmix operates on a long song, the entire waveform passes through one LSTM. If we split the inference into N segments, having N independent LSTMs that only saw 1/Nth of the waveform cannot replicate the behavior of the single LSTM!

Streaming LSTM architecture

Encoder/decoder: independent of length

In the Open-Unmix architecture, every layer except the LSTM (which is more of a module consisting of multiple layers, than a single layer itself) is independent of the length of the audio waveform.

Pseudocode illustration:

input_waveform = load_audio("my_song.wav")

# tensor of (2, N)
# represents 2-channel/stereo audio, N samples @ 44100 Hz sample rate
# i.e. N/44100 second duration

magnitude_stft = abs(stft(input_waveform))

# stft with fft_size=4096 i.e. 4096 output frequencies
# 2049 of them are non-redundant -> 2049 frequency bins
# tensor of (2, 2049, M)
# M time frames representing N time-domain samples processed with fft_size=4096 (or window=4096), overlap=1024

# some transformations: drop 2049th frequency bin
# interleave the two channels

x = tensor(4096, M) # input to open-unmix

There are ways to calculate how the N time-domain samples map to M STFT frames depending on the window size and overlap; in this case:

M = (N-4096)/(4096-1024)

The purpose of the first set of layers, fc1->bn1->tanh() activation is to do a first linear encoding of the 4096 frequency bins (representing two channels) into the hidden size of 1024:

x = tanh(bn1(fc1(x))

x = tensor(1024, M)

Note that the output is independent of the number of time frames M.

We can say the same after the LSTM in the middle: the final decoder layers are similar:

# discussing this next
x = lstm(x)
# skip conn, etc.

# linear->batchnorm->relu
x = relu(bn2(fc2(x)) 

x = tensor(..., M)

# linear->batchnorm
x = bn3(fc3(x))

x = tensor(4096, M)

By the end, we get back the same shape magnitude STFT as the input.

LSTM: dependent on length

Actually, my changes to my LSTM C++ code were not so dramatic. I won't cover how LSTM inference or LSTM details work, but from my browser history I may have looked at any of these sources to help: 1, 2, 3, 4.

Most of the heavy lifting was in the PyTorch documentation for the LSTM module and the related LSTMCell module for more step-by-step computation and updating of the LSTM.

The LSTM has 3 pieces of data it updates while it steps through an input sequence:

int hidden_state_size # lstm sizes
int cell_state_size   # lstm sizes
int seq_len           # size of input sequence

output_per_direction = tensor(seq_len, hidden_state_size)
output = tensor(seq_len, hidden_state_size)
hidden = tensor(hidden_state_size)
cell = tensor(cell_state_size)

So, stating the problem: how do we replicate the behavior of the LSTM output of long sequence using the LSTM output of K consecutive shorter sub-sequences?

The answer is, actually pretty easily.

This is how the old code used to work:

1. Given a long input sequence length
2. Create an LSTM (initializing the intermediate tensors output/hidden/cell to 0)
   • Recall that the output tensors are length-dependent, but not hidden or cell
3. Pass the input sequence through the LSTM, running the inference of the network
4. Return the long output sequence

Here's how the streaming LSTM code works:

1. Given a long input sequence length
2. Split it into shorter sub-sequences
3. Create a working buffer for the LSTM with the shorter sub-sequence length, with the intermediate tensors output/hidden/cell initialized to 0: struct lstm_buffers
4. Pass each sub-sequence through the LSTM alongside the reusable buffers: next_lstm_out = lstm(lstm_buffers, subsequence)
   • The crucial detail here is that while the shorter sub-sequence passes through the LSTM, the hidden and cell states are independent of sequence length, and by preserving them between each sub-sequence, the LSTM buffers will ultimately "have seen" (and included into its hidden and cell states) all of the long input sequence length

You can see how it works in my codebase with the following links to GitHub:

1. umx.cpp: main/entrypoint that prepares the reusable LSTM buffers: code
2. umx.cpp: passing the reusable LSTM buffers alongside each sub-sequence: code
3. inference.cpp: passing the reusable LSTM buffers to the LSTM forward inference function: code (think of this as the LSTMCell)
4. lstm.cpp: storing the hidden, cell, and output states in the reusable buffers to construct a longer-range view of the larger sequence: code

Conclusion

In the umx.cpp README, I show the demixing BSS scores with different combinations of my major architectural changes:

'Zeno - Signs', fully segmented (60s) inference + wiener + streaming lstm + uint8/16-quantized gzipped model file:

vocals          ==> SDR:   6.836  SIR:  16.416  ISR:  14.015  SAR:   7.065
drums           ==> SDR:   7.434  SIR:  14.580  ISR:  12.057  SAR:   8.906
bass            ==> SDR:   2.445  SIR:   4.817  ISR:   5.349  SAR:   3.623
other           ==> SDR:   6.234  SIR:   9.421  ISR:  12.515  SAR:   7.611

'Zeno - Signs', fully segmented (60s) inference + wiener + streaming lstm, no uint8 quantization:

vocals          ==> SDR:   6.830  SIR:  16.421  ISR:  14.044  SAR:   7.104
drums           ==> SDR:   7.425  SIR:  14.570  ISR:  12.062  SAR:   8.905
bass            ==> SDR:   2.462  SIR:   4.859  ISR:   5.346  SAR:   3.566
other           ==> SDR:   6.197  SIR:   9.437  ISR:  12.519  SAR:   7.627

'Zeno - Signs', unsegmented inference (crashes with large tracks) w/ streaming lstm + wiener:

vocals          ==> SDR:   6.846  SIR:  16.382  ISR:  13.897  SAR:   7.024
drums           ==> SDR:   7.679  SIR:  14.462  ISR:  12.606  SAR:   9.001
bass            ==> SDR:   2.386  SIR:   4.504  ISR:   5.802  SAR:   3.731
other           ==> SDR:   6.020  SIR:   9.854  ISR:  11.963  SAR:   7.472

Note that there is low impact to the demixing quality (0.02 dB lost in vocals, 0.2 in drums, 0.1 gained in bass, 0.2 gained in other). Overall it's a wash, and I consider this to be faithful inference (also from my various listening tests).

Comments