Migrating from Open-Unmix to Demucs in freemusicdemixer.com
GEMM convolutions, debugging, and performance improvements to implement Demucs inference in client-side WebAssemblyMigration
Migrated from the FreeMusicDemixer Blog, originally written on 2023-12-08
The entire site is based on Demucs now, so this announcement is now irrelevant on that site
Intro
The Demucs v4 Hybrid Transformer model has world-beating performance. The IEEE paper published by Facebook Research describes the model. In short, the Transformer architecture, originating from the famous Attention Is All You Need paper, is at the heart of a lot of powerful AI models, including ChatGPT.
In various demixing competitions, such as the Cadenza Challenge, Open-Unmix and Demucs are featured side-by-side as the academic, open-source baselines due to how they are developed openly and push forward the state of the art. For that reason, I'm happy to include both as the models of this site.
Demixing running times and scores
The base model available on this site is Open-Unmix, with the updated UMXL weights. For a song with a length of ~4 minutes ('Zeno - Signs') from the MUSDB18-HQ test set, here are the separation scores of Demucs compared to Open-Unmix.
Demucs v4 (on this site) takes 20 minutes (on my workstation) to achieve these scores:
vocals ==> SDR: 8.326 SIR: 18.257 ISR: 15.927 SAR: 8.311
drums ==> SDR: 10.041 SIR: 18.413 ISR: 17.054 SAR: 10.692
bass ==> SDR: 3.893 SIR: 12.221 ISR: 7.076 SAR: 3.237
melody ==> SDR: 7.432 SIR: 11.422 ISR: 14.161 SAR: 8.201
vocals ==> SDR: 6.830 SIR: 16.421 ISR: 14.044 SAR: 7.104
drums ==> SDR: 7.425 SIR: 14.570 ISR: 12.062 SAR: 8.905
bass ==> SDR: 2.462 SIR: 4.859 ISR: 5.346 SAR: 3.566
melody ==> SDR: 6.197 SIR: 9.437 ISR: 12.519 SAR: 7.627
The largest track from the MUSDB18-HQ test set, 'Georgia Wonder - Siren', around ~7 minutes long, ensures that this site can demix users' large tracks without crashing (by consuming more than the limit of 4 GB of memory).
Demucs v4 takes 40 minutes to achieve these scores:
vocals ==> SDR: 7.261 SIR: 13.550 ISR: 13.158 SAR: 6.763
drums ==> SDR: 10.629 SIR: 17.819 ISR: 17.373 SAR: 10.829
bass ==> SDR: 10.593 SIR: 19.696 ISR: 12.244 SAR: 10.007
meldoy ==> SDR: 6.324 SIR: 9.005 ISR: 13.223 SAR: 6.067
vocals ==> SDR: 5.858 SIR: 10.880 ISR: 14.336 SAR: 6.187
drums ==> SDR: 7.654 SIR: 14.933 ISR: 11.459 SAR: 8.466
bass ==> SDR: 7.256 SIR: 12.007 ISR: 10.743 SAR: 6.757
melody ==> SDR: 4.699 SIR: 7.452 ISR: 9.142 SAR: 4.298
Open-Unmix vs. Demucs: stats
This table shows a comparison of the two and also differences in how they are implemented on this site (or, from their characteristics).
| Open-Unmix | Demucs v4 | |
|---|---|---|
| Overall SDR (signal-to-distortion ratio) | 5.3 | 9.0 |
| Architecture | Linear encoder/LSTM/linear decoder | Convolution encoder/Transformer/convolution decoder |
| Input/output | Magnitude spectrogram (STFT) | Time domain (waveform) + complex spectrogram (STFT) |
| Lines of C++ code | 2364 | 4549 |
| Model weight size | 45 MB (quantized + compressed with low impact) | 81 MB (no quantization or compression) |
An interesting consequence of the LSTM of Open-Unmix vs. the Transformer of Demucs is that Demucs is parallelizeable in a way that Open-Unmix isn't. This means that future releases of this site can implement a parallel, multi-threaded version of Demucs, since separating an isolated subsection of the track has no bearing on demixing other subsections of the track.
The LSTM (long-short-term memory) of Open-Unmix requires that the song is fed forward and backward through the network for full demixing quality. To that end, I did implement a streaming LSTM, such that the entire track did not need to be stored in memory and crash by consuming > 4 GB. However, it still requires the song to be fed forward and backward in order.
Debugging during the development process
Writing the code for demucs.cpp was more challenging than umx.cpp, given the nature of Demucs and its more complex architecture.
Over the course of the development, the most important tool in my toolbox was to print detailed stats of the tensors at every step of the network:
Debugging tensor!: x_enc_1
shape: (1, 96, 128, 336)
min: -0.28594133257865906
max: 0.2303868532180786
mean: -2.4751065211603418e-05
stddev: 0.05556473508477211
sum: -102.19140625
min idx: (0, 55, 0, 1)
max idx: (0, 9, 0, 1)
FINISHED DEBUG FOR TENSOR x_enc_1
These let me eyeball the values passing through the network at each step and figure out where to track down errors during the implementation phase.
GEMM everywhere (especially in the convolutions)
Generalized Matrix Multiply (GEMM) is, as stated by this NVIDIA post:
GEMMs (General Matrix Multiplications) are a fundamental building block for many operations in neural networks, for example fully-connected layers, recurrent layers such as RNNs, LSTMs or GRUs, and convolutional layers.
In short, the best way of ensuring a neural network runs fast is by representing every operation as a matrix multiplication.
The original code for my convolution function used a for-loop approach:
template<int in_channels, int out_channels, int kernel_height, int kernel_width, int stride_height, int stride_width, int pad_height, int pad_width, int dilation_height, int dilation_width>
Eigen::Tensor3dXf conv2d(const Eigen::Tensor3dXf &x, const Eigen::Tensor4dXf &w, const Eigen::Tensor1dXf &b)
{
int in_height = x.dimension(1);
int in_width = x.dimension(2);
int out_height = static_cast<int>(std::floor(in_height + 2 * pad_height -
kernel_height) /
stride_height) +
1;
int out_width =
static_cast<int>(std::floor(in_width + 2 * pad_width - kernel_width) /
stride_width) +
1;
Eigen::Tensor3dXf y_out(out_channels, out_height, out_width);
// Initialize y_out to b
for (int chout = 0; chout < out_channels; ++chout)
{
y_out.chip<0>(chout).setConstant(b(chout));
}
// 2d convolution loop
for (int n = 0; n < kernel_width; ++n)
{
for (int m = 0; m < kernel_height; ++m)
{
for (int chin = 0; chin < in_channels; ++chin)
{
for (int j = 0; j < out_width; ++j)
{
for (int i = 0; i < out_height; ++i)
{
for (int chout = 0; chout < out_channels; ++chout)
{
int ih = i * stride_height + m * dilation_height -
pad_height;
int jw = j * stride_width + n * dilation_width -
pad_width;
if (ih >= 0 && ih < in_height && jw >= 0 &&
jw < in_width)
{
y_out(chout, i, j) += x(chin, ih, jw) * w(chout, chin, m, n);
}
}
}
}
}
}
}
return y_out;
}
Notice the template parameters: what this means is since the different convolution calls in Demucs use repetitive parameters, we define templated parameters such that the compiler can generate optimized versions of the code. This got some of my runtimes for convolution operations down from 5 seconds to 2 seconds during my benchmarking.
Eventually, I had to figure out the GEMM implementation of convolution, and that was crucial in getting Demucs running in under 1 hour.
The first function is im2col, which spreads the convolution pixels of interest into a matrix to be multiplied by the weights:
template<int kernel_height, int kernel_width, int stride_height, int stride_width, int pad_height, int pad_width, int dilation_height, int dilation_width>
inline Eigen::MatrixXf im2col(const Eigen::Tensor3dXf& input) {
// Adjust the calculation of height_col and width_col for dilation
int in_channels = input.dimension(0);
int height_col = (input.dimension(1) + 2 * pad_height - dilation_height * (kernel_height - 1) - 1) / stride_height + 1;
int width_col = (input.dimension(2) + 2 * pad_width - dilation_width * (kernel_width - 1) - 1) / stride_width + 1;
int in_height = input.dimension(1);
int in_width = input.dimension(2);
Eigen::MatrixXf output(height_col * width_col, in_channels * kernel_height * kernel_width);
output.setZero();
for (int c = 0; c < in_channels; c++) {
for (int kh = 0; kh < kernel_height; kh++) {
for (int kw = 0; kw < kernel_width; kw++) {
for (int h = 0; h < height_col; h++) {
for (int w = 0; w < width_col; w++) {
int h_pad = h * stride_height + kh * dilation_height - pad_height;
int w_pad = w * stride_width + kw * dilation_width - pad_width;
if (h_pad >= 0 && h_pad < in_height && w_pad >= 0 && w_pad < in_width) {
output(h * width_col + w, c * kernel_height * kernel_width + kh * kernel_width + kw) = input(c, h_pad, w_pad);
}
}
}
}
}
}
return output;
}
After im2col, the actual convolution multiplication becomes an easy one-liner:
template<int in_channels, int out_channels, int kernel_height, int kernel_width, int stride_height, int stride_width, int pad_height, int pad_width, int dilation_height, int dilation_width>
Eigen::Tensor3dXf conv2d_gemm(const Eigen::Tensor3dXf &x, const Eigen::Tensor4dXf &w, const Eigen::Tensor1dXf &b) {
int in_height = x.dimension(1);
int in_width = x.dimension(2);
// Calculate output dimensions
int out_height = static_cast<int>(std::floor(in_height + 2 * pad_height - kernel_height) / stride_height) + 1;
int out_width = static_cast<int>(std::floor(in_width + 2 * pad_width - kernel_width) / stride_width) + 1;
// Apply im2col
Eigen::MatrixXf im2col_matrix = im2col<kernel_height, kernel_width, stride_height, stride_width, pad_height, pad_width, dilation_height, dilation_width>(x);
// Reshape weights
// reverse last 3 axes (out chanel x in chan x kernel height x kernel width -> out chan x (kernel width x kernel height x in chan))
Eigen::Tensor4dXf w_swapped = w.shuffle(Eigen::array<int, 4>({0, 3, 2, 1}));
// then flatten to the last axis
Eigen::Tensor2dXf reshaped_weights_tensor = w_swapped.reshape(Eigen::array<int, 2>{out_channels, in_channels * kernel_width * kernel_height});
Eigen::MatrixXf reshaped_weights = Eigen::Map<Eigen::MatrixXf>(reshaped_weights_tensor.data(), reshaped_weights_tensor.dimension(0), reshaped_weights_tensor.dimension(1));
// Perform matrix multiplication with GEMM
Eigen::MatrixXf result = im2col_matrix * reshaped_weights.transpose();
// Add bias to each column of the result matrix
for (int chout = 0; chout < out_channels; ++chout) {
result.col(chout).array() += b(chout);
}
// Reshape result to 3D output tensor
Eigen::Tensor3dXf y_out(out_channels, out_height, out_width);
y_out.setZero();
for (int chout = 0; chout < out_channels; ++chout) {
for (int h = 0; h < out_height; ++h) {
for (int w = 0; w < out_width; ++w) {
int row_idx = h * out_width + w;
// Assign the value from the GEMM output to the output tensor
y_out(chout, h, w) = result(row_idx, chout);
}
}
}
return y_out;
}
An expected tradeoff of representing operations with GEMM is overusing memory - but we could afford it, so it was worth it.
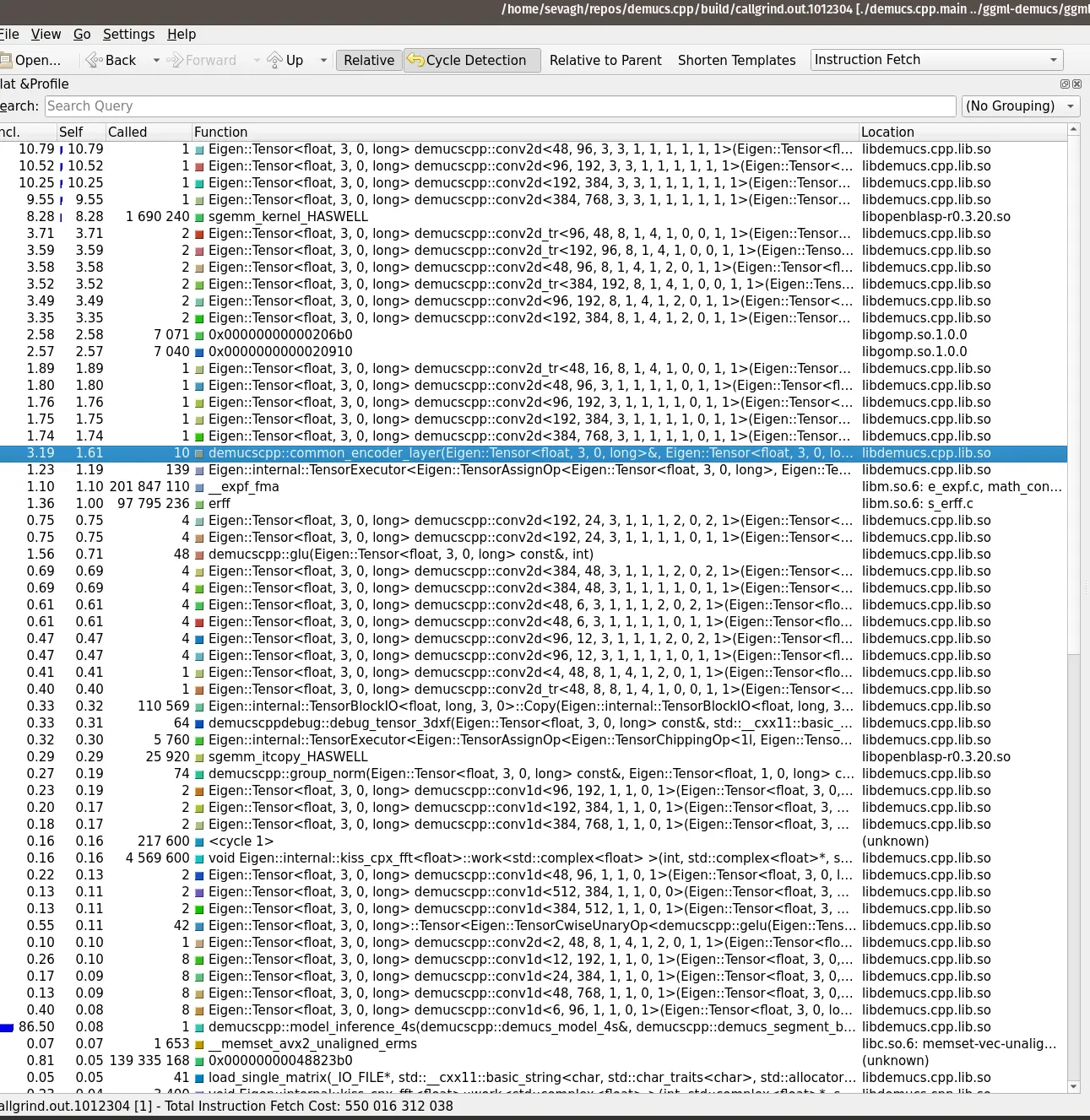
One of the last profiling runs of demucs.cpp shows how so much time is spent in GEMM, which is a good thing: I'm basically crunching as much numbers as possible on the CPU, and not wasting time doing other operations: